1.自由空間伝搬損失(Γ0)
Γ0=(4πd/λ)2
d:距離 λ:波長(299.8/f(MHz) )(m)
2.スパン損失(Ls)
送受信アンテナが等方性アンテナでないとき
送信側の出力端子の電力(Pt)と受信側の入力端子の電力(Pr)との間の
伝送損失はスパン損失(Ls)と呼ばれ、次式で表されます。
Ls=Pt/Pr=(Lt・Lr/(Gt/Gr))・Lo・X
Pt :送信機出力
Pr :受信機入力
Lt,Lr
:送信および受信給電系損失
Gt,Gr
:送信および受信アンテナ利得
Γ :伝搬損失
X
:アンテナ効果(主ビームとのずれによる減衰)
3.実効伝搬損失(Γe)
電波伝搬は自由空間伝搬損失(Γo)に大地の影響による損失
が加わり、またアンテナに対する大地の影響も加わる。
したがって、実際の伝搬損失は自由空間損失にこれらの影響を
加味したものとなるが、ややこしくなるのでここでは便宜上、
Γe=Γo とする。
これらの概念を下図に示す。
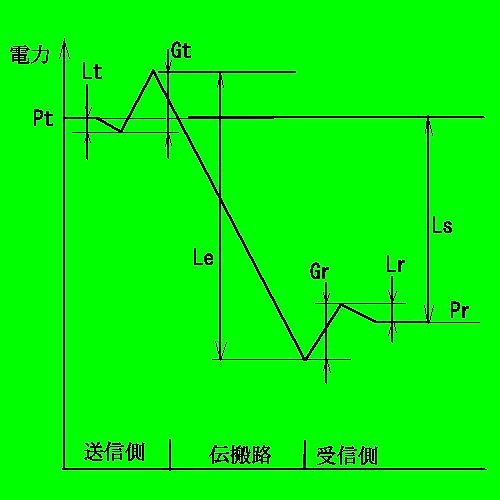
電波伝搬の概念を示すレベルチャート
4.フレネルゾーン
送信点(T)から受信点(R)に向かう平面波の途中、受信点から(b)の
距離にある波面上の各点からRに対する効果は波面上の各点がRに及
ぼす2次波の効果の総和に等しいとされている。
送信点(T)と受信点(R)を結ぶ直線上の点(C)を含む波面上において
R,C間の距離を(r)とすると、rより、λ/2,2λ/2,3λ/4,・・・・mλ/2
だけ遠い点の軌跡は同心円を描く。このλ/2ずつづれた波面は互いに
受信点Rに対し、反対の効果を及ぼす。また、1つおきのものは互いに
強め合う効果をもたらす。
第一のゾーンの半径をr1とすると
(b+λ/2)2=b2+r12
r12=bλ+λ2/4 λ2/4<bλ,λ2/4<r12
r1=√(bλ)
第二ゾーン、第三ゾーンの半径をr2,r3とすると、同様に
r2=√(2bλ),r3=√(3bλ)
第mゾーンの半径は
rm=√(mbλ) となる。
それぞれのゾーン半径r1,r2・・に対応する円の面積はπbλ、2πbλ、
3πbλ・・・mπbλと近似できる。したがって、 円環状の各ゾーンの
面積はπbλとなる。(実際は、外側のゾーンに行くに従って、上記の近
似分だけ少しずつ大きくなる。)
下図のようなゾーンが考えられる。
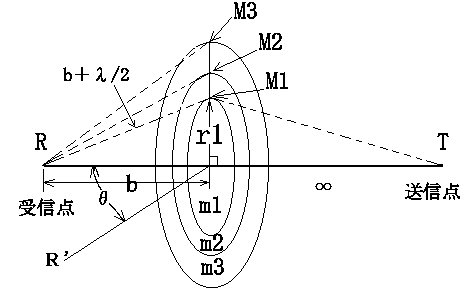
それぞれのゾーンが受信点に及ぼす効果は、その面積に比例し、受信
点にいたる距離に反比例する。また半径の増大に伴い角度の補正を受
ける。
波面に垂直な方向(受信点R方向)を基準とした任意方向の2次波の
効果は次式に比例して減少する。
(1+COSθ)/2
従って、正面方向では1、θ=±90°では1/2、後方θ=180°
では0になる。
m1とm2、m2とm3・・・など、隣り合うゾーンは互いに反対の作用を
及ぼす各ゾーンの合成効果は以下のようになる。
S=m1ーm2+m3-m4・・・・・・
=m1/2+(m1/2-m2+m3/2)+(m3/2-m4+m5/2)+・・
各ゾーンの物理的意味から、かっこ内はそれぞれ0になるので
S=m1/2 に近似できる。
つまり、全波面が及ぼす合成効果はゾーン間の打ち消しのために
第1ゾーンだけの効果の概ね1/2になる。
第1ゾーンのみの効果は全波面の(無障害)の全効果の2倍になる。
上記の考察から、第1ゾーンのみの伝搬では無障害伝搬の2倍
(+6dB)になる。次に第2ゾーンを含めた伝搬では最初の極小値を
とる。これを、繰り返しながら、自由空間伝搬に収束する。
回折損失を考えるとき、障壁により遮られるゾーンにより信号強度
が変動する。第1ゾーンが隠れるまで障壁の高さがあがると信号は
急激に低下する。これは上記で述べた第1ゾーンが隠れるためである。
この回折領域について以下に記す。
5.回折損失
回折のある伝搬路の受信電界強度をEr、回折の原因が無いときの電界
強度をEoとすると、回折係数Zは Z=Er/Eo 定義される。
切り立った直線のエッジと電波通路のクリアランスをhcとすると、
クリアランス係数uは
u=hc/r1 で表される。h1の符号は見とおし内を+とする。
一般に第mフレネルゾーンの半径rmは
rm=r1・√m
となり、第mフレネルゾーンに接する障害物のクリアランス係数は
u=±√m となる。
受信点において利用できるエネルギーは電界強度の2乗に比例する。
回折のない電界強度をEo、回折のあるときの電界強度をErとすれば、
Eo2/Er2は回折による電力損失比になる。
回折損失Ldは Ld=Eo2/Er2=1/Z2
Ld(dB)=-20logZ(dB)
となる。
ナイフエッジが、第1、第2、第3のフレネルゾーンに接するとき、uは
1、√2、√3になるので、
Z1=1.15 (+1.2 dB)
Z2=0.89 (-1.05dB)
Z3=1.1 (+0.8 dB) となる。
奇数次のフレネルゾーンに接するときは利得、偶数次のフレネルゾーン
に接するときは損失になる。
第1フレネルゾーンを完全に隠す領域(u<-1)では電界強度は|u|に
反比例して減少する。近似式は以下のとおりである。
Z=|1/(2πu)|
Ld(dB)=20log|u|+16 (dB)
参考:マイクロウェーブ電波伝搬 コロナ社 (渋谷茂一 執筆、黒川廣二監修)